The P vs NP problem is a major unresolved issue in theoretical computer science.

It challenges our fundamental understanding of computation, efficiency and the nature of problem-solving itself.

This question doesn’t just examine what computers can do today. It probes the limits of what machines can achieve, and what they may never be able to do.

In this blog post, we’ll unravel the mystery of P vs NP, and look at some code examples in the Go programming language along the way to help illuminate the problem.

What Is P vs NP?

Before diving into technicalities, let’s think about the problem in very general, and easily accessible, terms.

Let’s imagine that we’re solving a puzzle.

For some puzzles, the process of finding the solution is as straightforward as following a set of rules, and, by doing so, you can reasonably expect to solve them in a short amount of time.

These are problems in the class P, which stands for “polynomial time”.

In simple terms, polynomial time means that as the size of the problem (for example, the amount of data used as input) grows, the time it takes to solve the problem increases at a predictable and manageable rate.

For example, if an algorithm takes time proportional to the square of the input size (n²) or the cube of the input size (n³), it’s considered to be in polynomial time.

So a problem being in class P means there exists an algorithm that can solve the problem efficiently — within a time frame that grows polynomially with the size of the input.

Now consider a different category of puzzles. These puzzles may take an astronomically long time to solve, especially as they grow larger, but once a solution has been presented, verifying its correctness is quick and easy.

These belong to the class NP, which stands for “nondeterministic polynomial time”.

It’s as if we had some kind of magical “guessing machine” that can instantly propose a solution, leaving us with the much simpler task of checking its validity.

The core question of P vs NP is deceptively simple: are these two classes the same?

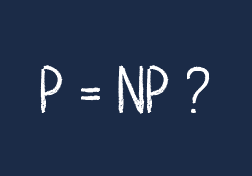
In other words, is every problem that can be quickly verified also one that can be quickly solved?

Despite decades of research, no one has been able to definitively answer this question. It remains one of the most famous open problems in mathematics and theoretical computer science.

However, there’s a great incentive on offer, because anyone who comes up with a generally accepted solution to the P versus NP problem could win one million dollars as part of the Millennium Prize offered by the Clay Institute, a charitable foundation that supports mathematical research.

Writing Code in Go to Help Us Think About The P vs NP Problem

At first glance, using the Go programming language might seem an unlikely way to explore such an abstract question.

After all, Go prides itself on being an eminently practical language — clean, concise and optimised for real-world software engineering challenges.

However, Go’s simplicity means that we can quickly write some code that will help us to illustrate the fundamental ideas underlying the P vs NP problem.

Solving a P Problem

So let’s start with an example. Consider the problem of sorting a list of integers, a very basic computational task.

Sorting is a problem in the P class because there exist well-known algorithms, like quicksort or mergesort, that can solve it efficiently.

Writing a sorting function in Go is straightforward, as shown below:

package main

import (
	"fmt"
	"sort"
)

func main() {
	numbers := []int{42, 7, 13, 99, 18}

	sort.Ints(numbers)

	fmt.Println("Sorted list:", numbers)
}

Here, the sort.Ints function sorts the list in polynomial time relative to its size (by default, using a version of the pdqsort algorithm, which, on average, runs in O(n log n), i.e. polynomial time).

No surprises there. Sorting is quintessentially a P problem: we have a clear and efficient algorithm available for solving it.

Solving an NP Problem

Now let’s contrast this with a problem in the NP class: the Travelling Salesman Problem (TSP).

In the TSP, a salesman must visit a list of cities exactly once, returning to the starting point while minimising overall the amount of travel he does.

This deceptively simple task becomes computationally intractable as the number of cities grows, simply because the number of possible routes explodes exponentially.

Verifying a proposed solution to the TSP is straightforward. Given a candidate route, we can compute the total cost and check whether it meets the requirements.

But finding the optimal route? Well, that’s not so easy.

The best-known algorithms for solving the TSP rely on techniques that effectively try all possible routes, which is computationally expensive.

To illustrate this, let’s write some Go code that naively attempts to solve the Travelling Salesman Problem by applying brute force:

package main

import (
	"fmt"
	"math"
)

var bestCost = math.MaxFloat64

func calculateCost(route []int, distances [][]float64) float64 {
	totalCost := 0.0

	for i := 0; i < len(route)-1; i++ {
		totalCost += distances[route[i]][route[i+1]]
	}

	totalCost += distances[route[len(route)-1]][route[0]] // return to start

	return totalCost
}

func permute(route []int, distances [][]float64, left int) {
	if left == len(route)-1 {
		if cost := calculateCost(route, distances); cost < bestCost {
			bestCost = cost
		}

		return
	}

	for i := left; i < len(route); i++ {
		route[left], route[i] = route[i], route[left]
		permute(route, distances, left+1)
		route[left], route[i] = route[i], route[left]
	}
}

func main() {
	distances := [][]float64{
		{0, 10, 15, 20},
		{10, 0, 35, 25},
		{15, 35, 0, 30},
		{20, 25, 30, 0},
	}

	cities := []int{0, 1, 2, 3}

	permute(cities, distances, 0)

	fmt.Println("The cost of the shortest route:", bestCost)
}

The permute function in the code above generates all possible permutations of the cities in order to explore every potential route.

It uses a recursive backtracking approach. Starting at a given index (held within the left parameter), it swaps the current city with each of the remaining cities and recursively calls itself to generate further permutations.

When the recursion reaches the end of the route (i.e. when left equals the last index), the function calculates the cost of the current route by calling the calculateCost function.

If the route's cost is lower than the current value of the bestCost variable, it updates this variable with the cost of the better route that has just been found.

After evaluating a route, the function swaps the cities back to restore the original state for the next iteration, maintaining correctness.

So, as we have seen, the program contained in the example code above uses a brute-force approach, generating all possible permutations of cities to find the shortest route.

While it works well for small inputs, it quickly becomes infeasible as the number of cities grows, demonstrating the fundamental difference between P and NP problems.

Real-World Complexity

In practice, solving NP problems like the TSP often involves heuristic algorithms, which aim for good enough solutions found in a reasonable amount of time, rather than the absolute perfection provided by a brute-force approach.

Consider a genetic algorithm or a heuristic like simulated annealing: these approaches don’t guarantee the optimal solution, but they can produce high-quality solutions far more efficiently than brute force.

Simulated annealing is inspired by the physical process of annealing in metallurgy. It seeks to find good solutions by simulating the gradual cooling of a material, which allows atoms to reach a state of minimal energy.

In computational terms, this involves starting with a high probability of accepting worse solutions to escape local minima, gradually reducing this probability as the algorithm progresses toward convergence.

A genetic algorithm, on the other hand, mimics biological evolution. It begins with a population of potential solutions, applying operators like selection, crossover and mutation to evolve these solutions over generations.

The goal of a genetic algorithm is to converge on high-quality solutions by combining and refining traits from previous candidates.

Implications of the P vs NP Problem

The resolution of the P vs NP question carries profound implications.

If P were equal to NP, it would inevitably revolutionise our understanding of the power of computation.

Problems that seem intractable today, like protein folding or optimising supply chains, could become soluable with ease.

However, most computer scientists believe that P does not equal NP, meaning there are problems whose solutions inherently require super-polynomial time, even as verifying a proposed solution remains efficient.

This assumption underpins much of modern cryptography. For instance, algorithms like RSA depend on the difficulty of factoring large numbers, a problem assumed to be computationally extremely difficult for classical computers.

Should P equal NP, these foundational cryptographic schemes would collapse, as their security guarantees rely on the infeasibility of efficiently solving such problems.

This fragility underscores the profound implications of resolving the P vs NP question, which extends far beyond the mere theoretical curiosity of academic computer scientists.