I’m going to show you one of the simplest methods available to secure a message, making it harder for unwitting observers to read. A cipher is a word used for a method that allows text to be encrypted or decrypted — in other words, made harder to read and then restored to an original form.

What Is a Caesar Cipher?

This particular example, the Caesar cipher, gained its name because it seems that the famous Roman general Julius Caesar used this method to keep his private messages secure on the battlefield. It is a form of substitution cipher, because every letter in the text that you want to encrypt is substituted by another letter.

The basic rule in a Caesar cipher is to shift each letter one or more places forwards (or sometimes backwards) in the alphabet: for example, if you shift each letter forwards once, A becomes B, B becomes C, C becomes D, and so on, until you get to Z, which becomes A, because the shift wraps around the alphabet, starting again at the beginning once you’ve reached the end.

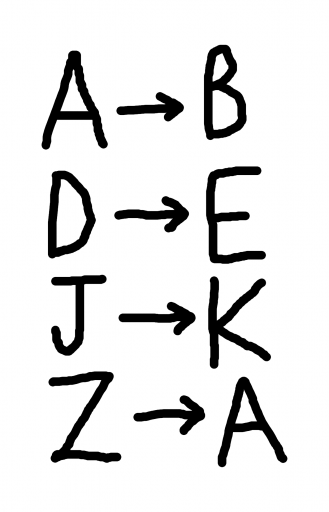
So if you wanted to encode the phrase “THIS IS A TEST” using the cipher described above, the result would be “UIJT JT B UFTU”. Of course, you can easily see how each of the letters has moved forwards one place in the alphabet: this is easiest to see in the case of the single letter A, which becomes B, as we predicted it would above.

Shifting Letters in Go

So how would we write code in the Go programming language to move a single letter (which, in our code, we will call a rune)? Each rune in Golang has a numerical Unicode value; in fact, the rune data type is simply an alias for an int32. So we can increment each rune by one in order to get the value for the following letter in the alphabet, as we do in the example below:

package main

import (
	"fmt"
)

func caesarCipherShiftRune(r rune) rune {
	return r + 1
}

func main() {
	fmt.Printf("%c\n", caesarCipherShiftRune('A')) // B
	fmt.Printf("%c\n", caesarCipherShiftRune('B')) // C
	fmt.Printf("%c\n", caesarCipherShiftRune('C')) // D
	fmt.Printf("%c\n", caesarCipherShiftRune('M')) // N
	fmt.Printf("%c\n", caesarCipherShiftRune('T')) // U
	fmt.Printf("%c\n", caesarCipherShiftRune('Z')) // [
}

This works perfectly for almost all the letters of the alphabet, as you can see from the print outs if you run the code above. (Also be aware of how we use "%c" with the format.Printf function, so that the rune gets printed out as a character, rather than as a numeric value.) But it fails in the case of the letter Z, because our function doesn’t wrap around to A: it simply moves on to the next character, which in the Unicode (or ASCII) character set happens to be an opening square bracket.

Making Our Runes Wrap Around

So we need to improve our function. First of all, we need to subtract the value of the first rune in our alphabet, 'A', from the rune that we are given as an argument. This will give a value from 0 to 25 inclusive for every letter in the alphabet (whereas the actual numeric value of 'A' is 65, so we would otherwise have a value from 65 to 90 inclusive).

We can then increment the resulting value and then do a modulus operation, in order to ensure that the result rolls over properly. We will do r % 26, because there are twenty-six letters in the standard upper-case English alphabet. Finally, we add the value of 'A' to the result before we return it, so that we have the proper Unicode values, rather than starting from zero, as we temporarily needed to do. Our updated function is below:

package main

import (
	"fmt"
)

func caesarCipherShiftRune(r rune) rune {
	return (((r - 'A') + 1) % 26) + 'A'
}

func main() {
	fmt.Printf("%c\n", caesarCipherShiftRune('A')) // B
	fmt.Printf("%c\n", caesarCipherShiftRune('Z')) // A
}

Success! We now roll over to the first letter, A, when we reach the final letter, Z, as we had originally intended. We now have a function that can allow us to encrypt single runes. But, of course, we’re unlikely to want to send a single-letter message. We’re more likely to want to send some text that is stored as a string.

Working With Strings

However, we can now easily use this function to iterate over the runes in a given string, producing an encrypted message by concatenating the modified runes to an output string:

package main

import (
	"fmt"
)

func caesarCipherShiftRune(r rune) rune {
	return (((r - 'A') + 1) % 26) + 'A'
}

func main() {
	const input = "THIS IS A TEST"
	var output string

	for _, r := range input {
		if r >= 'A' && r <= 'Z' {
			r = caesarCipherShiftRune(r)
		}

		output += string(r)
	}

	fmt.Println(output) // UIJT JT B UFTU
}

You will see that I have also include a validation check within the range loop, so that only valid English-language letters are passed to the encryption function, because, of course, we don’t want to shift the spaces in our input, since our code is only set up to handle the 26 letters of the alphabet. But that’s all we need to modify, because only these letters, not other characters, tend to contain important information that we want to keep secret.

Shifting the Letters More Than Once

We’re doing well, but, so far, we have only moved the letters forward one place. What if want to decide how many places we want to shift by whenever we call our helper function? We can do that by creating another argument, which we will use as the increment, rather than hard-coding it as 1.

package main

import (
	"fmt"
)

func caesarCipherShiftRune(r rune, shift uint) rune {
	s := rune(shift % 26)

	if s == 0 {
		return r
	}

	return (((r - 'A') + s) % 26) + 'A'
}

func main() {
	const input = "THIS IS A TEST"
	var output string

	for _, r := range input {
		if r >= 'A' && r <= 'Z' {
			r = caesarCipherShiftRune(r, 13)
		}

		output += string(r)
	}

	fmt.Println(output) // GUVF VF N GRFG
}

Notice how I have converted the initial uint to a rune, so that we can use it in our calculation with the other rune. I also perform a modulus operation on it, so that it can never be more than 25, which is the greatest number of shifts possible, since shifting 26 times is equivalent to shifting 0 times. There is then a validation check, which simply returns the initial rune, if we are supposed to shift by no places.

Completing the Caesar Cipher

We’ve done the hard work now, so we can simply tie all of this together, creating separate functions to encrypt and decrypt a given string using the Caesar cipher:

package main

import (
	"fmt"
	"strings"
)

func caesarCipherShiftRune(r rune, shift uint) rune {
	s := rune(shift % 26)

	if s == 0 {
		return r
	}

	return (((r - 'A') + s) % 26) + 'A'
}

func caesarCipherEncrypt(value string, shift uint) string {
	var builder strings.Builder
	value = strings.ToUpper(value)

	for _, r := range value {
		if r >= 'A' && r <= 'Z' {
			r = caesarCipherShiftRune(r, shift)
		}

		builder.WriteRune(r)
	}

	return builder.String()
}

func caesarCipherDecrypt(value string, shift uint) string {
	return caesarCipherEncrypt(value, 26-(shift%26))
}

func main() {
	const encryptShift = 18
	const input = "THIS IS A TEST"

	encrypted := caesarCipherEncrypt(input, encryptShift)
	decrypted := caesarCipherDecrypt(encrypted, encryptShift)

	fmt.Printf(
		"INPUT: %s\nENCRYPTED: %s\nDECRYPTED: %s\nINPUT EQUALS DECRYPTED: %t\n",
		input, encrypted, decrypted, input == decrypted,
	)
}

Decrypting is easy: we just do exactly the same thing as we do when encrypting but with a different shift value. So we only need to call caesarCipherEncrypt in our caesarCipherDecrypt function. The shift value needed to decrypt a message is the exact opposite of the one used to encrypt it: we can calculate that by subtracting the initial shift value by the number of potential values (26 in our case, the total number of letters in the alphabet). We also use a modulus operation to make sure that we never produce a result lower than zero — which, in the case of a uint, would overflow.

Conclusion

I have exported these functions in a package on Github, so you can use them in your own code or call them via a command-line application, if you ever want to make your messages more secret. The Caesar cipher makes use of a wonderful algorithm that is easy to understand (and, of course, very easy for serious cryptographers to crack), yet it still performs the vital job of securing confidential communications, just as it did for the Roman general Julius Caesar and his soldiers in the first century BC.

When you want to pass a message on to someone, you have to give them the encrypted version, but you also need them to be aware of how many times you’ve shifted the letters, so they can correctly decrypt it. Perhaps you’ll agree in advance what shift-value you’ll be using and then just send the messages when you need to communicate. The ancient Roman historian Suetonius tells us that Julius Caesar would always shift his encrypted texts by three places.

Because there are only 26 possible values for the shift parameter, however, a malicious eavesdropper who wanted to access your original messages without your permission could simply produce all of the 26 possible output messages and find the one that actually makes sense (since the others, very probably, wouldn’t be made up of intelligible words). This is a simple example of a brute-force attack.

Extra Credit

Before I go, I’ll leave you with one final exercise that you can complete on your own. Our final code handles upper-case English letters, and it converts lower-case English letters to their upper-case equivalents, so that all decrypted messages will always be upper-case. That works fine for most messages, because it’s the content that really matters, not the way it’s presented. But what if we wanted to keep the original case (so that, for example, the people decrypting the messages can more easily distinguish between the names of people and other nouns)? See if you can modify the caesarCipherShiftRune function so that it handles both upper- and lower-case letters separately.