What Is Conway’s Game of Life?
Language
- unknown
by James (Golang Project Structure Admin)
This post will discuss the Game of Life, which is:
- a zero-player game, famous in the history of computing;
- a cellular automaton;
- a deterministic system that follows a simple ruleset;
- a creation of the British mathematician John Conway.
Don’t worry if you don’t entirely understand what all those terms mean, because we’re going to go through them in more detail below, before you get chance to actually explore the game for yourself.
Table of Contents
What Is a Zero-Player Game?
It’s easy to understand what a two-player game is. Pong was one of the first video games that could be played by two people, batting a ball back and forth between each players paddles. It was intended to simulate tennis, which is a two-player game played in the real world with bats, a ball and a net.
Even before personal computers were first invented, board games like chess and card games like gin rimmy could be played across a dining-room table by two people taking turns. These games follow simple rules (although, as we’ll see, that doesn’t mean that they’re necessarily simple to play), which make them ideal for converting into computer games.
With the emergence of the Internet, massively multiplayer online (MMO) games became possible, allowing many thousands — or even millions — of people from around the world to take part in the same virtual experience: World of Warcraft is a well known example.
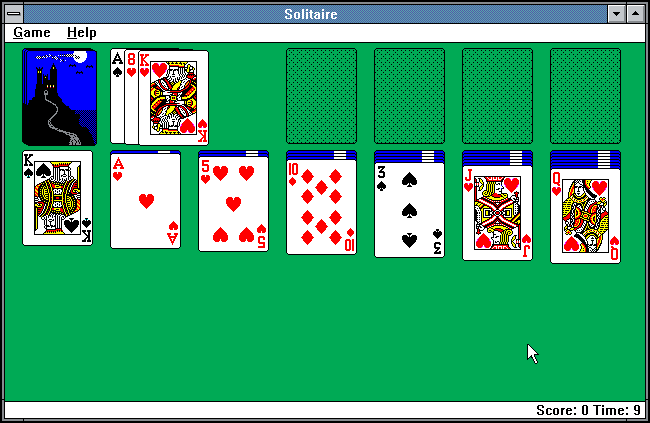
One-player games can be played alone by a single person. The most obvious example is the card game known as solitaire (or patience). A software version of solitare was released in 1990 by Microsoft to showcase the capabilities of its new Windows 3.0 operating system, one of the first to feature a graphical user interface (GUI).
Many modern console and computer games are one-player, like, to take just two examples, Assassin’s Creed or The Elder Scrolls V: Skyrim. Many other major video games have both two-player (or multiplayer) and one-player versions, allowing gamers to spend time playing on their own but also take part in missions or competitions with friends online.
But the idea of a zero-player game can seem somewhat strange and counterintuitive. There is an obvious question: how is the game even played if no one actually plays it?
A zero-player game evolves naturally over time based on rules that it rigidly follows as it moves from one state to another. It requires no input from a player, except perhaps to set an initial state that will then progress naturally on its own. In the case of a zero-player video game, the gameplay is performed by the computer itself.
What Is a Deterministic System?
A deterministic system is like a black box that has clearly defined inputs and outputs: the same inputs will always produce the same outputs. So all modern computers are deterministic systems, because their operation can be predicted, depending upon how we interact with them.
However, computers can also work with inputs that are unpredictable, meaning that the output will also be unpredictable. One example of this is when a truly random-number generator uses sensors to detect sound or temperature fluctuations in the outside environment, feeding them into its algorithm in order to ensure unpredictable output.
However, more often, computers will just use a pseudorandom-number generator, which uses an algorithm that is complex but technically deterministic, meaning that the next number could be predicted if you understood the input used to seed the generator and the algorithm used. This is also known as a deterministic random bit generator: it is good enough for most purposes, but it would not be used where true randomness is required, such as when writing code that picks lottery-winning numbers.
In the Go standard library, the "math/rand" package allows for the generation of pseudorandom numbers, while the "crypto/rand" package can generate truly random numbers, using a non-deterministic algorithm.
So when we say that Conway’s Game of Life is deterministic, we just mean that it follows a clear set of rules, and that every iteration of its evolution can always be perfectly predicted from the previous iteration. This is precisely what makes it so interesting, because it allows us to see how very simple rules can give rise to complex patterns.
Is the Universe Deterministic?
Philosophers also talk about determinism, which is the belief that the universe, and everything in it, follows clear and unchanging rules, meaning that, if this view is true, whatever is now occurring in the world can be explained by prior causes — at least in theory, if not necessarily in practice.
In other words, if we had been able to understand everything that it’s possible to know about those causes and how they interact with each other, we would have been able to predict whatever is currently happening in the world, from wars to weather systems.
That is, of course, a bold claim, but it’s one that has been attractive to many philosophers and scientists, perhaps because intellectuals like to put their trust in reason and rationality as supreme guides to truth.
For example, Newtonian physics — which was the dominant model of the universe from the time of Isaac Newton (1642–1727) up until Albert Einstein (1879–1955) — is deterministic, because the laws of nature were thought to be explained entirely by equations that describe how forces such as gravity work.
This model allowed physicists and astronomers to make incredibly accurate predictions, such as that Halley’s comet will be visible from Earth only once every 75 or 76 years.

This type of philosophical and physical determinism has one big problem, however. If all events are triggered by prior causes, what caused the very first event at the beginning of the universe?
Since religion held great sway over people’s lives and minds in earlier centuries, it was simply assumed that God had set everything in motion. We now live in more sceptical times, and we’re used to challenging the explanations put forward by religious and other authorities, so this is less likely to be accepted as an easy solution as it was in the past.
The birth of quantum physics also unsettled old ideas about determinism, since particles at a subatomic level seem to be following strange rules that are not entirely predictable. But this is only a stepping point on the search for truth, because physicists are currently trying to find a theory that will supersede our current understanding, the so-called theory of everything. As such, it remains an open question whether we’re living in a deterministic universe or not.
This very short and simplified overview of philosophical determinism is not meant to be an exhaustive exploration of the concept: it is just intended to show that what we’ve been discussing also has a much wider context outside the realms of computer science.
If you want to undertake a more rigorous exploration of the subject, I suggest that you look at the relevant entry in the Stanford Encyclopedia of Philosophy. You may also want to research the interesting topic of free will and consider whether or not it’s possible for this to exist in a deterministic universe.
But if you only remember one thing about determinism, just remember that it involves a system (either one that tangibly exists, like the universe, or a virtual one, like our game) controlled by strict rules that can be used to make accurate predictions about future states (or, indeed, past ones) of that system. There are no events or occurrences that break those rules.
What Is a Cellular Automaton?
A cellular automaton (the plural is automata) is a specific type of zero-player game. It is made up of a grid — or gameboard — of square cells.
In the case of the Game of Life, we use a two-dimensional grid, but the concept can be extrapolated to higher dimensions (or even a single dimension, using one long line of cells). So you can think of it just like a traditional board game, where each square on the board can be identified by a pair of coordinates — for example, if we have a 8 by 8 grid, then the cell in top-left corner could be (0,0) and the cell in the bottom-right corner could be (7,7).
What makes this grid interesting, however, is that it has a set of rules that determine its behaviour. That is why it is called an automaton (which is a word sometimes used to describe simple robots).
Each cell has a particular state — think of it as a particular attribute, or a set of attributes — and, every time that the gameboard is updated, each state can change based on rules that rely on the states of neighbouring cells.
If we want to put that more mathematically, then we could say that the state of a cell at iteration i is equal to the output of a function that takes as its input the set of the states of neighboring cells at i-1.
What do we do at iteration 0 then, since there is no iteration -1 for us to use as input to the function? Of course, the gameboard will be set manually on the first iteration, or else some state will be randomly (or otherwise) generated for it.
What happens on the first iteration is precisely what makes a cellular automaton a type of game (because players have the ability to set an initial state) and what happens on subsequent iterations is what makes it zero-player (because there is no more interaction as the cells evolve on their own, i.e. autonomously).
How exactly the rules work on the input to produce the output will differ depending on the individual implementation of a cellular automaton. But any kind of cellular automata will always have a ruleset that takes that input to produce an output state for each of the cells.
The polymath John von Neumann is often credited with having first created the concept of cellular automata, all the way back in the 1940s. His work was stimulated by his interest in understanding better how biological evolution generates creatures with increasing complexity over millions of years.
What Are the Rules of the Game of Life?
As mentioned above, our gameboard consists of a grid of square cells: each one can be either alive or dead. The evolutionary lifecycle of each cell over the course of the game depends on the state of its neighbouring cells.
Each cell has eight neighbours, including those cells that touch diagonally. If it helps, you can think of the eight cardinal points of a compass — north, north-east, east, south-east, south, south-west, west and north-west — because in each of those directions there is a neighbouring cell.
The original gameboard is intended to be of theoretically infinite size. That isn’t practical in real life, so implementations will often choose a fixed size for the board and consider the top-left neighbour of the top-left cell to be the bottom-right cell (i.e. the cells at the edge of the board wraparound). It is also possible to create an implementation with a border at the edge, where cells touching the border have fewer neighbours, meaning that their behaviour is more limited than other cells.
However, the general rules are easy to understand. If a cell is currently alive, it can be killed by overpopulation if more than three of its neighbouring cells are also alive; likewise, it can be killed by underpopulation if fewer than two of its neighbouring cells are alive. If a cell is currently dead, it can come back to life by reproduction if exactly three of its neighbouring cells are alive.
The three simple rules listed above (i.e. overpopulation, underpopulation and reproduction) are enough to create all of the complex interactions and beautiful patterns that you will see emerge in the game.
John Conway called these rules “genetic laws”, since they determine the birth, death and and survival of life in each cell.
Indeed, you can see the game as encapsulating a simple form of natural selection, the evolutionary process understood to biologists as the generator of all life on Earth, since not all of the cells will survive or reproduce. There is, however, little scope for mutation, which is the process that has allowed animals to adapt to their environment, since cells in the Game of Life can only be in one of two states, alive or dead.
If you don’t like the biological analogies, you can simply think in terms of boolean logic: each cell is either on or off (or one and zero, or true and false) and never anything in between.
At a lower level, if you think of the electronic circuit boards of the processors used in the machine that you’re using to read this text, a high voltage is used to represent any on state and a low voltage is used to represent off. Computers are naturally adapted to binary representations.
It’s possible to use this knowledge to your advantage when implementing a computer version of Game of Life: for example, you could use a uint32 variable in Go to represent a row of thirty-two different cells, with each bit in the number being set if the corresponding cell is alive and unset if it’s dead. I haven’t built my version of the cellular automaton in this way, but it’s an interesting way to represent the data efficiently.
Who Was John Conway?
John Conway was a lecturer in mathematics at the University of Cambridge when he created the Game of Life, which would be responsible for giving him a certain degree of fame around the world.
But he’d had a keen interest in mathematical problems since he was a young child: the story may be apocryphal, but his mother claimed that he could recite the powers of two — 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384 and so on — at fours years of age. These numbers are, of course, of great interest to computer scientists, since computers use binary encoding (which is why RAM, for example, will often be sold with memory capacities that are a power of two).
He did his undergraduate and research degrees at Cambridge. His early interest in exponential numbers clearly continued to grow, because he focused his postgraduate work on number theory and managed to solve an open problem set by his supervisor, proving that every positive integer can be written as the sum of no more than 37 fifth powers.

After studying von Neumann’s work on cellular automata, John Conway devised the Game of Life. It first gained wider attention and interest after being discussed in a column called Mathematical Games written by the mathemagician Martin Gardner for the October 1970 edition of Scientific American.
He first worked on the game using graph paper and stone counters, arduously plotting each iteration by hand and thinking about the patterns that emerged.
Conway always had somewhat of a love-hate relationship with the famous cellular automaton he created, perhaps embarrassed that he should be so well remembered for what seemed to be such relatively minor work and not for his more “serious” mathematics. However, his work in recreational mathematics can only have helped to share the immense passion he had for his discipline with many others who hadn’t devoted themselves to the world of numbers in the same way that he was able to.
John Conway later went to work at Princeton University in the United States, where he was appointed to the John von Neumann Chair of Mathematics, which is particularly appropriate since, as we have already mentioned, von Neumann was perhaps the first person to clearly define the concept of a cellular automaton as we would understand it today.
In 2020, John Conway died at the age of 82 after having been diagnosed with COVID-19. It may have lost its creator, but the Game of Life continues.
Where Can I Play Conway’s Game of Life?
The strictly correct answer to this question is that you can’t play it anywhere, since John Conway’s Game of Life is a game that is not meant to be actively played. However, we can informally talk about playing the game, meaning that we choose (or randomize) an initial condition and simply watch as it evolves over time.
I have created an online version of Conway’s Game of Life that is hosted on Itch, which means that it is publicly accessible for anyone to explore and experiment with. It was written in TypeScript and transpiled down to JavaScript. Click here to have a look at it.
Before you begin, press the “Controls” button in order to find out how to set cells, clear the grid and perform many other simple operations.
If you use a physical gameboard and counters to play the Game of Life in the real world, you may have to use a special system (like the one Martin Gardner discusses in his original article) or possess an extremely good memory when moving the counters from one iteration to the next, because the new state of the board is determined by the neighbouring cells on the board’s old state, but you may end up changing the old state as you go along, thereby introducing mistakes in the process.
However, it’s easier to get around that problem when writing code: I simply use a double-buffering technique, by creating two separate arrays, one that contains the old state of each cell on the gameboard and another that represents the new state.
When the board is updated, I only ever update the buffer array, while only ever reading information from the array that actually contains the state currently shown on screen; then I swap them, so that the buffer array becomes the next visible one, and the old visible one is left to be used as a buffer in the next iteration.
Below is an image of the Typescript method that is used to populate the two arrays when the game first begins:
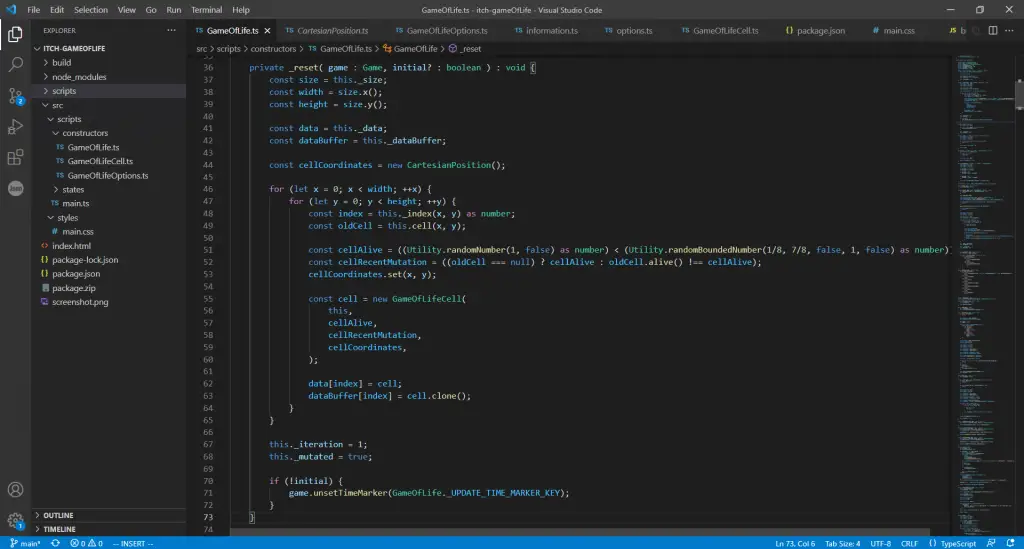
You can see how each GameOfLifeCell is initially set to be either alive or dead based on randomly generated numbers (in this case, using the crypto.getRandomValues function provided by the browser, rather than the older Math.random). The user can, however, pause the game and clear the gameboard in order to set each cell individually, if they prefer.
What Sort of Patterns Tend to Emerge in the Game of Life?
We saw above how simple the rules are that define the evolution of the cells that make up the gameboard in John Conway’s Game of Life.
However, don’t be mistaken into believing that simple rules must also produce simple behaviour: complex patterns of behaviour can often occur — as an emergent property — from the very simplest sets of rules.
Just think about how easy it is to learn the basic rules of chess, perhaps the most famous boardgame in the world, and yet how hard it is to become a grandmaster who understands the myriad subtleties of the game. It can decades of intense study to understand the complex gameplay that emerges from the simple rules of chess.
Likewise, unexpected, interesting and even beautiful patterns can emerge from the operation of the Game of Life‘s three simple rules.
Some patterns will stay stable, not evolving from one iteration to the next (unless they’re disrupted by the lifecycles of nearby cells), and these patterns were termed “still lifes” by John Conway, obviously by analogy with the artistic term.
The easiest “still life” to recognize is perhaps the two-by-two square. If this is created, or emerges through evolution, it will continue to exist through subsequent iterations of the game, exhibiting no further evolution.

There are other more complicated still lifes, some of which will appear quite commonly and many others extremely rarely. For example, in one of Martin Gardner’s books, there is an example of a “billiards table”, which is a large rectangle of cells with contiguous circles of cells (looking like the pockets of the table used to play pool or snooker or billiards), and this is completely static once it has been created.
Other patterns will appear to move across the gameboard. For this reason, they are known as “spaceships”. The most of famous of these is the “glider”, which is shown in the image above (to the right of the square). Its shape evolves and after four iterations it will have returned to the original shape, having moved one cell to the southwest. So we can easily predict that after twenty iterations it will have moved diagonally a distance of five squares.
Some clever soul has even managed to create a fully working digital clock that operates based on the logical interactions of cells in the Game of Life. Gliders are used to transmit information from cell to cell. You can view the YouTube video that shows how it looks below, but don’t ask me how they managed to work out how to set the whole thing up, because I must admit that it’s far beyond my comprehension!

Very good article.Really thank you! Really Cool.
Thanks for commenting. I’m glad you enjoyed reading the article, and I hope you got chance to play with the interactive game I created too!